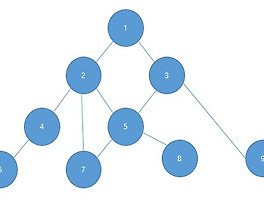
Delete
자식 노드가 없는 경우 그냥 삭제한다.
자식 노드가 1개인 경우
부모와 자식이 각각 1개이므로 선형적인 형태이다. 삭제하려는 노드의 부모와 삭제하려는 노드의 자식을 이어주면 된다.
자식 노드가 2개인 경우
해당 노드를 삭제하고 다른 곳의 노드 값을 넣는다. predecessor, successor를 넣어야 한다.
자식이 2개이므로 오른쪽 서브트리의 최소값이 successor가 된다.
그 successor의 자식이 없다면 그냥 삭제하면 되고, 1개라면 자식을 successor의 위치에 넣는다.
tree_delete(T,z):
if left[z] == None or right[z] == None: #자식 노드가 없는 경우 삭제.
y=z
else:
y = tree_successor(z) #자식이 있다면 successor를 찾는다
if left[y] != None: successor의 왼쪽 자식이 없다면
x = left[y]
else:
x = right[y]
if left[y] != None: #왼쪽 자식이 있다면
x = left[y] #x는 왼쪽 자식
else: #오른쪽 자식이 있다면
x = right[y] #x는 오른쪽 자식
if x!=None: #x가 비어있지 않다면
p[x] = p[y] #y의 부모를 x의 부모로.
if p[y] == None: #y가 루트라면
root[T] = x
elif y == left[p[y]]: #y가 왼쪽 자식이라면
left[p[y]] = x # y부모의 왼쪽 자식 자리에 x 넣음
else:
right[p[y]] = x #y 부모의 오른쪽 자식 자리에 x 넣음
if y!=z: #삭제하려는 값이 successor와 다르다면
key[z] = key[y] #successor를 삭제하려는 값의 위치에 넣는다.
return y
이진 검색 트리의 시간 복잡도는 O(logn)이다. 최악의 경우 skewed tree가 나온다면 O(n)이다.
균형잡힌 트리 - 레드블랙트리, 키 삽입이나 삭제 시 추가로 트리의 균형을 잡아줌으로써 높이를 O(logn)으로 유지
'알고리즘' 카테고리의 다른 글
| 초간단 python DFS Depth First Search 깊이 우선 탐색 (2) | 2018.11.20 |
|---|---|
| 초간단 python BFS Breadth First Search 너비 우선 탐색 (0) | 2018.03.21 |
| 이진 검색 트리 2 (0) | 2018.02.13 |
| 이진 검색 트리 (0) | 2018.02.12 |
| 트리와 이진트리 (0) | 2018.02.12 |