graph={
1:[2,3],
2:[1,4,5,7],
3:[1,5,9],
4:[2,6],
5:[2,3,7,8],
6:[4],
7:[5,2],
8:[5],
9:[3],
}
def BFS(graph,root):
visited=[]
queue=[root]
while queue:#while queue is not empty
n = queue.pop(0)
if n not in visited:#if n is not in visited list.
visited.append(n)#put the n to the visited list.
for i in graph[n]:#the numbers i connected with n
if i not in visited:#i is not in visited list.
queue.append(i)#put the i to the queue.
return visited
print(BFS(graph,1))
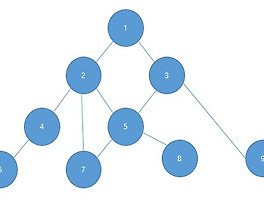
파이썬으로 짠 위 BFS 코드에서 쓰인 그래프
출처 인프런 강의 https://www.inflearn.com/
MIT 강의 https://www.youtube.com/watch?v=s-CYnVz-uh4
그래프 탐색의 응용
웹 크롤링 : 웹 크롤러는 조직적, 자동화된 방법으로 www을 탐색하는 프로그램, 검색 엔진과 같은 사이트에서 데이터를 최신 상태로 유지하기 위해 웹 크롤링을 함
SNS 친구의 친구 찾기
네트워크 방송
garbage collection 쓰레기 수집 : 메모리 관리 기법 중 하나, 프로그램이 동적으로 할당했던 메모리 영역 중 필요 없게 된 영역을 해제
model checking
checking mathematical conj
solving puzzles & games
Pocket Cube 2x2x2
configuration graph
vertex for each possible state of cube
edge for possible move
Graph representation:
Adjacency lists : array Adj of |v|, linked lists
for each vertex uEV, Adj[u], Adj[u] stores u's neighbors
BFS
visit all nodes reachable from given s E V
O(V+E)
BFS(s, Adj):
level = {s:∮}
parent = {s:None}
i=1
frontier = [s] #level i-1
while frontier:
next = [] #level i
for u in frontier:
for v in Adj[u]:
if v not in level:
level[v] = i
parent[v] = u
next.append(v)
frontier = next
i+=1
handshaking lemma
무방향 그래프 : 노드의 차수의 합은 간선의 수의 2배
방향 그래프 : 노드 차수의 합은 간선의 수와 같다
순회 (traversal) : 그래프의 모든 노드들을 방문하는 일
1. BFS Breadth First Search 너비 우선 순회
2. DFS Depth First Search 깊이 우선 순회
BFS 알고리즘은 다음순서로 노드들을 방문
L0 = {s}, s는 출발 노드
L1 = L0의 모든 이웃 노드들
L2 = L1의 이웃들 중 L0에 속하지 않는 노드들
...
Li = Li-1의 이웃들 중 Li-2에 속하지 않는 노드들
출발점인 s에서부터 바깥으로 나아감
큐를 이용한 너비 우선 순회
level order traversal은 BFS의 이진트리 버전이다. 루트에서 시작해서 자식 노드를 방문하고 손자 노드를 방문한다.
시작 점을 확인하고 그 노드(1)를 큐에 넣는다.
큐가 비어있지 않다면 큐에서 1을 pop한다.
체크되지 않은 1의 이웃 노드들(2,3)을 체크하고 큐에 넣는다.
2를 큐에서 빼내고 이웃한 노드인 4,5를 체크하고 큐에 넣는다.
3을 빼내고 이웃한 노드인 7,8을 체크하고 큐에 넣는다.
4를 빼내고 이웃한 노드는 없다.
5를 빼내고 이웃한 노드인 6을 체크하고 큐에 넣는다.
7을 빼내고 이웃한 노드가 없다.
8을 빼내고 이웃한 노드가 없다.
6을 빼내고 이웃한 노드가 없다. 큐가 비어있으므로 while문이 종료된다.
노드의 방문 순서는 한가지가 아니다.
BFS(G,s) #그래프 G와 출발 노드 s
Q<-∮
Enqueue(Q,s)
while Q!=∮ do
u<-Dequeue(Q)
for each v adjacent to u do
mark v as visited
Enqueue(Q,v)
BFS와 최단경로
s에서 Li에 속한 노드까지의 최단 경로의 길이는 i이다.
입력 : 방향 혹은 무방향 그래프 G=(V,E) 출발노드 s E V
출력 : 모든 노드 v에 대해서
d[v] = s로부터 v까지의 최단 경로의 길이 (edge 개수)
π[v] = s로부터 v까지의 최단경로상에서 v의 직전 노드
BFS(G,s)
Q<-∮
d[s]<-0 #s에서 s까지의 거리는 0
π[v]<-None #s의 직전 노드는 없음
Enqueue(Q,s)
while Q!=∮ do
u<-Dequeue(Q)
for each v adjacent to u do
if v is unvisited:
mark v as visited
d[v]<-d[u]+1 #v까지 거리
π[v]<-u #u는 v의 직전 노드
Enqueue(Q,v)
BFS(G,s)
Q<-∮ #비어 있는 큐
for each node u do
d[u]<- -1 #노드에 아직 방문하지 않음
π[u]<- None #직전 노드 없음
d[s]<-0 #시작점 방문하지않음
π[s]<-None #시작점의 직전 노드는 없음
Enqueue(Q,s) #시작점을 큐에 넣음
while Q!=∮ : #큐가 비어있지 않다면 반복
u<-Dequeue(Q) #큐에 있는 노드를 u에 대입
for each v adjacent to u do #u의 이웃인 v에 대해
if d[v] == -1: #v가 아직 방문되지 않았다면
d[v]<-d[u]+1 #이전 길이에 1을 더한 값이 시작점으로부터의 거리가 됨
π[v]<-u #직전 노드는 당연히 u가 됨. u로부터 v에 도달했으므로.
Enqueue(Q,v) #u의 이웃 노드인 v를 큐에 넣음
인접 행렬로 구현할 경우 시간 복잡도는 O(n^2)
인접리스트로 구현할 경우 시간 복잡도는 O(n+m)
출발 노드로부터의 거리와 직전 노드
BFS 트리
각 노드 v와 π[v]를 연결하는 에지들로 구성된 트리
BFS 트리에서 s에서 v까지의 경로는 s에서 v까지 가는 최단 경로
너비 우선 순회 : 최단 경로 출력하기
print_path(G,s,v)
if v==s: #v가 출발점이라면
print s #출발점 출력
elif π[v]==None: #이전 노드가 없다면
print "no path from s to v exists" #가는 길이 없다고 출력함
else:
print_path(G,s,π[v]) #재귀 함수로 s에서부터 v까지 출력, 목적지 v에서부터 한칸씩 뒤로 가다가 s를 만나면 s에서 v까지 출력
print v
그래프가 연결되어 있지 않거나 방향 그래프라면 BFS에 의해 모든 노드가 방문되지 않을 수도 있음
BFS_ALL(G)
while there exists unvisited node v:
BFS(G,V)
'알고리즘' 카테고리의 다른 글
| Binary Search Tree BST 이진 탐색 검색 트리 파이썬 python (0) | 2018.11.21 |
|---|---|
| 초간단 python DFS Depth First Search 깊이 우선 탐색 (2) | 2018.11.20 |
| 이진 검색 트리 3 (0) | 2018.02.13 |
| 이진 검색 트리 2 (0) | 2018.02.13 |
| 이진 검색 트리 (0) | 2018.02.12 |