 초간단 python DFS Depth First Search 깊이 우선 탐색
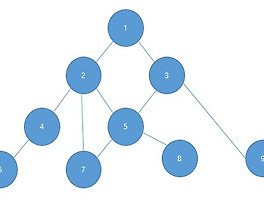
graph={ 1:[2,3], 2:[1,4,5,7], 3:[1,5,9], 4:[2,6], 5:[2,3,7,8], 6:[4], 7:[5,2], 8:[5], 9:[3], } def DFS(graph,root): stack=[root] visited=[] while stack: n=stack.pop() for i in graph[n]: if i not in visited: stack.append(i) if n not in visited: visited.append(n) print('v',visited) return visited print(DFS(graph,1))파이썬으로 짠 위 DFS 코드에서 쓰인 그래프 [1, 3, 9, 5, 8, 7, 2, 4, 6] 강의 영상
초간단 python DFS Depth First Search 깊이 우선 탐색
graph={ 1:[2,3], 2:[1,4,5,7], 3:[1,5,9], 4:[2,6], 5:[2,3,7,8], 6:[4], 7:[5,2], 8:[5], 9:[3], } def DFS(graph,root): stack=[root] visited=[] while stack: n=stack.pop() for i in graph[n]: if i not in visited: stack.append(i) if n not in visited: visited.append(n) print('v',visited) return visited print(DFS(graph,1))파이썬으로 짠 위 DFS 코드에서 쓰인 그래프 [1, 3, 9, 5, 8, 7, 2, 4, 6] 강의 영상
 초간단 python BFS Breadth First Search 너비 우선 탐색
graph={ 1:[2,3], 2:[1,4,5,7], 3:[1,5,9], 4:[2,6], 5:[2,3,7,8], 6:[4], 7:[5,2], 8:[5], 9:[3], } def BFS(graph,root): visited=[] queue=[root] while queue:#while queue is not empty n = queue.pop(0) if n not in visited:#if n is not in visited list. visited.append(n)#put the n to the visited list. for i in graph[n]:#the numbers i connected with n if i not in visited:#i is not in visited list. queue.a..
초간단 python BFS Breadth First Search 너비 우선 탐색
graph={ 1:[2,3], 2:[1,4,5,7], 3:[1,5,9], 4:[2,6], 5:[2,3,7,8], 6:[4], 7:[5,2], 8:[5], 9:[3], } def BFS(graph,root): visited=[] queue=[root] while queue:#while queue is not empty n = queue.pop(0) if n not in visited:#if n is not in visited list. visited.append(n)#put the n to the visited list. for i in graph[n]:#the numbers i connected with n if i not in visited:#i is not in visited list. queue.a..
트리와 이진트리
계층적인 구조를 표현조직도, 디렉토리, 가계도 트리는 노드(node)와 링크(link)로 구성됨맨 위의 노드는 루트(root), 노드들을 연결하는 선을 link, edge, branch라고 부름 어떤 노드 A의 아래에 노드 B가 있으면 노드 A는 B의 부모 노드이고 B는 A의 자식 노드이다.부모가 동일한 노드는 형제(sibling) 관계이다.루트 노드를 제외한 트리의 모든 노드들은 유일한 부모 노드를 가진다.자식이 없는 노드는 리프(leaf) 노드 서브(sub)트리 : 트리의 어떤 부분을 잘라내도 트리다.레벨 : root 노드의 레벨을 0이라고 하면 아래로 내려갈 수록 1, 2, 3 ... n 레벨이 된다. root 노드의 레벨을 1이라고 하면 아래로 내려갈 수록 2, 3, 4, ... n이 된다. 트리..